n个数字（0,1,…,n-1）形成一个圆圈，从数字0开始，每次从这个圆圈中删除第m个数字（第一个为当前数字本身，第二个为当前数字的下一个数字）。当一个数字删除后，从被删除数字的下一个继续删除第m个数字。求出在这个圆圈中剩下的最后一个数字。

Solution-1:

模拟.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int Josephus(int n, int m) {
    boolean [] childs = new boolean[n];
    int i = 0, step = 0, cnt = n;
    while(cnt>0){
        if(!childs[i]) {
            ++step;
            if(step % m == 0){
                childs[i] = true;
                --cnt;
            }
        }
        i = (i+1) % n;
    }
    return i == 0? n-1: i-1;
}

Solution-2:

找规律.

1
2
3
4
5
6
// 递归
public int Josephus(int n, int m) {
    if(n == 0) return -1;
    if(n == 1) return 0;
    else return (Josephus(n-1, m) + m) % n;
 }

1
2
3
4
5
6
7
8
9
// 迭代
public int Josephus(int n, int m) {
    if(n == 0) return -1;
    int last = 0;
    for(int i= 2;i<=n;++i){
        last = (last + m) % i;
    }
    return last;
}

Solution-2规定f(n=0)返回-1, 这个是题目自身规定的, 表示没有元素要删除. 如果 n>0, 那么只需要f(n=1)这一个边界就可以了. f(n=0)无论取值多少, 都能得到 f(n=1) = 0, 因为 f(n=1) = (f(n=0) + k) % 1, 任何数对1取模都等于0.

公式含义

题目本身并不重要, 重要的是要理解递归公式的含义.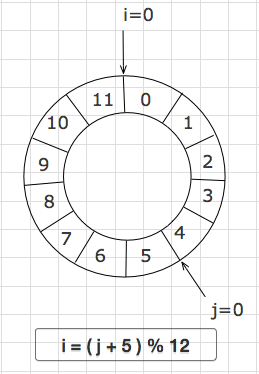

对于上图中的环形数组, 有两个指针i 和 j, 两个指针的起始位置不同, j 比 i 滞后了5个位置(或者说 i 比 j 滞后了7个位置), 因为是环形的, 所以可以从 j 推导出 i. i = (j +5) % 12 或者 j = (i+7) % 12.理解了环形数组的索引官话规律, 就能很容易理解约瑟夫问题中的递推公式了.

#变式-1: 小孩报数问题
Description

有N个小孩围成一圈，给他们从1开始依次编号，现指定从第W个开始报数，报到第S个时，该小孩出列，然后从下一个小孩开始报数，仍是报到S个出列，如此重复下去，直到所有的小孩都出列（总人数不足S个时将循环报数），求小孩出列的顺序。
Input

第一行输入小孩的人数N（N<=64）
接下来每行输入一个小孩的名字(人名不超过15个字符)
最后一行输入W,S (W < N)，用逗号”,”间隔
Output

按人名输出小孩按顺序出列的顺序，每行输出一个人名
Sample Input

1
2
3
4
5
6
7
5
Xiaoming
Xiaohua
Xiaowang
Zhangsan
Lisi
2,3

Sample Output

1
2
3
4
5
Zhangsan
Xiaohua
Xiaoming
Xiaowang
Lisi

Solution:

递归方法只能计算出最后一个出列小孩的位置, 但本题要求计算出出列的顺序, 很难应用递归, 只能采用模拟了.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import java.io.*;
import java.util.*;

public class Main {
    public static Scanner in = new Scanner(new BufferedReader(new InputStreamReader(System.in)));//this is faster than new Scanner(System.in)
    public static PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));

    static String[] names = new String[64];
    static int N, W, S;
    public static void main(String[] args) {
        N = in.nextInt();
        for (int i = 0; i < N; ++i) names[i] = in.next();

        String[] W_S = in.next().split(",");

        W = Integer.valueOf(W_S[0]);
        S = Integer.valueOf(W_S[1]);
        // 下面的过程就是经典的约瑟夫环模拟解法.
        boolean[] found = new boolean[N];
        int step = 0, cnt = 0, idx = W - 1;
        while (cnt < N) {
            if(!found[idx]){
                ++step;
                if (step % S == 0) {
                    found[idx] = true;
                    out.println(names[idx]);// 找到一个小孩
                    ++cnt;
                }
            }
            idx = (idx + 1) % N;
        }
        out.flush();
    }
}